AVRマイコンをUbuntu上で開発しよう、という試み。
といっても先駆者が結構たくさんいるので
玉虫色に染まれ!さんの手順をそのまま実行すれば問題なく動作するかも。
http://d.hatena.ne.jp/over80/20090302/1236006771
統合開発環境はありません。曰く、
"「初めに言いますが、いわゆる「統合開発環境」的なものはありません。そういったものが欲しい人は素直にWindowsで開発していた方が幸せでしょう。Linuxでやろうと思う人は「エディタは自分の好きなものを使わせろ!」とか「GUIだといちいちマウスに持ち替えなきゃあかんやろ。CUIでやらせろ!」とか言い出すような人です。"
ということみたいです。
Ubuntuに限らずLinuxを敢えて利用するってことはそれなりの信念があるのでしょう。
もちろん主にコマンドでの操作です。
詳細は続きから。
2012年11月18日日曜日
2012年11月4日日曜日
lagrange補間
離散した複数の点を結ぶlagrange補間法。
あんまり実用的でないらしい。
ソース内で複数の点(x,y)を設定し、プログラムを実行することで補間すべき点(x,y)を列挙したファイルlag_dat.i10と補間曲線上の適当な刻み幅の点(x,y)を列挙したファイルlag_dat.o10を作成。
また、それをgnuplot上に描画するためのプロットファイル*.pltを作成する。
lagrange補間は任意の数の点(x,y)を滑らかな曲線でつなぐ関数を求める。
2点なら直線で繋げる、3点なら2次曲線で繋げる、4点なら3次曲線で繋げる、といった事象を利用している。
説明もそこそこに以下リスト。
indent FILENAME -kr -i8
を使うと幸せ。
indent FILENAME -kr -i8
を使うと幸せ。
label
課題
2012年8月30日木曜日
DCモータのPWM制御
最近のモータ制御では主流となっているPWM(Pulse Width Modulation)での制御をしてみた。
目的は
大昔の授業でマイコン制御のサンプルとして持ってきてもらったので良い実験材料かと。
で、まあ必要なのがボリュームの位置を読むAD変換と、
出力用のPWMという訳で。
PWM自体はやったことあったので2時間あれば組みきれると思ったら大間違い。
原因はプログラム特有の問題(オーバーフロー)だったりモータ特有の問題(突入電流など)だったり。
まず、手持ちでAD変換ができるチップがATMEGA88Pだったのでこれを使用。
データシートを見ると11番(PD5)と12番(PD6)がPWMの出力端子で、
23〜28番(PC0〜PC5)がAD変換用に使える。
PWM用の端子もたくさんあるみたいだけど今回はOC0xしか使わないので。
モータードライブにはTOSHIBAのTA8428K(S)を使用。
なければ自作でフルブリッジドライバを作るほかない。
ドライバはIN1がHIGH、IN2がLOWで正転、
IN1がLOW、IN2がHIGHで逆転、
両方LOWで開放、
両方HIGHでブレーキだったような気がする。
詳しくはデータシートを。
可変抵抗は今回特に何でもいいので適当。
プログラムリストは続きから。
今回、最も詰まった注意点を先に。
まず、volatile unsigned long でvalue を宣言しているけど、
途中で割り込み排除したのでvolatileは多分不要。
あと、これはint型ではオーバーフローしてしまう(最大値を超えてしまう)ので、必ずlong型に。
これに気づかずボリュームを上げてるのに、ある点で急に回転数が低くなってしまった。
もうひとつはマイコンの電源をACアダプタから取っていて、
ACアダプタが3Aまで流せるんだけど、そこにモータつないでたのも失敗だった。
やっぱりドライバには別電源が必要だと感じた。
モータの突入時(通電時)には大電流が流れるので、PWM制御でモータを動かすときには、
秒間何回も突入が起きて動作が不安定になる。
もっとACアダプタの定格電流が大きければ問題ないかもしれないけど、
今回は3Aだったので突入電流によってアダプタが落ちていたかも。
これに一番苦労させられた。
モータの通電時にアダプタが落ちて、一瞬後に復旧するわけだけど、
このときも通電時なわけでまたアダプタが落ちる。
このせいでモータが動いたと思った瞬間止まって、また動いてを繰り返す。
今回はPWM制御が目的だったから、この反応がむしろ正常に見えてデューティに問題がないかなどのプログラム上の問題を探しに行ったりもした。
また、モータドライバで2V程度電圧が落ちるらしいので、モータ用には少なくとも5V程度はほしい。
定格は30Vなのでよくある箱型の9V電池を使用した。
なので電源とオーバーフローには注意。
とくにAVRのAD変換器の出力は10bit(1024通り)なので。
プログラムの大まかな流れは、
AD変換の出力が0〜1023なので、半分の511で区切り、
0〜511が逆転、512〜1023が正転となってる。
ただし、511近傍では信号を与えない停止状態となってる。
この近傍の広さがdefineにあるBRANGEの値。
あと今回は可変抵抗の出力を電圧として読む必要が無いので、
0〜1023のままで使ってる。
では、以下リスト。
目的は
1.モータをPWMでドライブする。
2.可変抵抗(ボリューム)で回転数が変えられる。
3.正転、逆転が可能。
の3つ。2.可変抵抗(ボリューム)で回転数が変えられる。
3.正転、逆転が可能。
大昔の授業でマイコン制御のサンプルとして持ってきてもらったので良い実験材料かと。
で、まあ必要なのがボリュームの位置を読むAD変換と、
出力用のPWMという訳で。
PWM自体はやったことあったので2時間あれば組みきれると思ったら大間違い。
原因はプログラム特有の問題(オーバーフロー)だったりモータ特有の問題(突入電流など)だったり。
まず、手持ちでAD変換ができるチップがATMEGA88Pだったのでこれを使用。
データシートを見ると11番(PD5)と12番(PD6)がPWMの出力端子で、
23〜28番(PC0〜PC5)がAD変換用に使える。
PWM用の端子もたくさんあるみたいだけど今回はOC0xしか使わないので。
モータードライブにはTOSHIBAのTA8428K(S)を使用。
なければ自作でフルブリッジドライバを作るほかない。
ドライバはIN1がHIGH、IN2がLOWで正転、
IN1がLOW、IN2がHIGHで逆転、
両方LOWで開放、
両方HIGHでブレーキだったような気がする。
詳しくはデータシートを。
可変抵抗は今回特に何でもいいので適当。
プログラムリストは続きから。
今回、最も詰まった注意点を先に。
まず、volatile unsigned long でvalue を宣言しているけど、
途中で割り込み排除したのでvolatileは多分不要。
あと、これはint型ではオーバーフローしてしまう(最大値を超えてしまう)ので、必ずlong型に。
これに気づかずボリュームを上げてるのに、ある点で急に回転数が低くなってしまった。
もうひとつはマイコンの電源をACアダプタから取っていて、
ACアダプタが3Aまで流せるんだけど、そこにモータつないでたのも失敗だった。
やっぱりドライバには別電源が必要だと感じた。
モータの突入時(通電時)には大電流が流れるので、PWM制御でモータを動かすときには、
秒間何回も突入が起きて動作が不安定になる。
もっとACアダプタの定格電流が大きければ問題ないかもしれないけど、
今回は3Aだったので突入電流によってアダプタが落ちていたかも。
これに一番苦労させられた。
モータの通電時にアダプタが落ちて、一瞬後に復旧するわけだけど、
このときも通電時なわけでまたアダプタが落ちる。
このせいでモータが動いたと思った瞬間止まって、また動いてを繰り返す。
今回はPWM制御が目的だったから、この反応がむしろ正常に見えてデューティに問題がないかなどのプログラム上の問題を探しに行ったりもした。
また、モータドライバで2V程度電圧が落ちるらしいので、モータ用には少なくとも5V程度はほしい。
定格は30Vなのでよくある箱型の9V電池を使用した。
なので電源とオーバーフローには注意。
とくにAVRのAD変換器の出力は10bit(1024通り)なので。
プログラムの大まかな流れは、
AD変換の出力が0〜1023なので、半分の511で区切り、
0〜511が逆転、512〜1023が正転となってる。
ただし、511近傍では信号を与えない停止状態となってる。
この近傍の広さがdefineにあるBRANGEの値。
あと今回は可変抵抗の出力を電圧として読む必要が無いので、
0〜1023のままで使ってる。
では、以下リスト。
2012年8月10日金曜日
USBメモリからMacbookAir2012にUbuntuをインストールする
前回(http://hamachan-pon.blogspot.jp/2012/07/macbookair2012ubuntu.html)、
USBフラッシュメモリを利用したUbuntuのインストールについて言及したので。
なお、MacbookAir2012でしか確認していないのでWin機や他のMacでも同様に動作するかは不明。
あと、大抵の場合にはCDドライブついてるのでそちらを利用するととても便利。
また、外付けCDドライブでもインストール可能みたいなので持っているならそちらを利用。
この記事は
「CDドライブの付いていないPCに外付けCDドライブを購入することなくUbuntuをインストールする」
ためのものです。
また、作業をUbuntuで行なっているのでMacに無いコマンドがあるかも…。
本題。
簡単な流れは、
1.Macでのセットアップ
2.USBインストールメディアの作成
3.インストール
となってます。
詳しくは以下。
1.Macを起動し、rEFItをインストール
rEFItをインストールすることで、起動時にOSやUSBメモリを選択することが可能になります。
インストールはこのあたり(http://refit.sourceforge.net/)から出来ます。
2.パーティションの分割
Macの上部のメニューから移動→ユーティリティ→HDD(SSD)のパーティションを選択。
Mac側を適当に減らして空き領域を作る。
この際、「Mac,空き領域,空き領域(4GB)」のように、4GB程度(実際にはメモリの2倍だっけ)のスワップ領域を作成することが推奨されてますが、なくても問題なく動くという話もあります。
3.Ubuntuインストールメディアの作成
まず、公式(http://www.ubuntu.com/download/desktop)からUbuntuのisoイメージをダウンロード。64bit対応してるのかよく知らないけど32bit。
ダウンロード先はデスクトップにしておくとわかりやすいかな。
端末を開いて、
このディレクトリで、
とする。
FILENAMEはisoイメージの名前。
これでisoイメージを変換する。
ここでUSBメモリを差し込む。端末から、
今回は(/dev/disk1)だった。
確認できたらアンマウント。端末から
手順2で使ったディスクユーティリティからUSBメモリのパーティションを変更。
USBメモリをフォーマットする。(FAT32で)
さっきと同様にアンマウント(されてるかも)
次のコマンドを実行。
確認したデバイスの頭にrが付いていることに注意。
(/dev/disk1→/dev/rdisk1)
書きこみ完了まで十数分かかります。
/dev/disk1に書きこむと気が遠くなるほど長いので注意。
書き込みが終わったらUSBメモリの取り出し。
4.Ubuntuのインストール
作成したUSBインストールメディアを挿したまま、コンピュータを再起動。
するとrEFItにより選択画面が出てくるのでUSBメモリ(Ubuntu)を選択。
画面の流れに沿ってキーバインドなどの設定を行う。
Ubuntuのインストール先をパーティション分けした空き領域に入れる。
マウントポイントは「/」です。
同様に4GBの空き領域にはswapを設定。
両方ともフォーマットはext4でよいです。
ブートローダのインストール先を/dev/sdaに設定。
インストールの実行。
以上です。
記憶で書いてるのでなかなか間違いも多いかも。
USBフラッシュメモリを利用したUbuntuのインストールについて言及したので。
なお、MacbookAir2012でしか確認していないのでWin機や他のMacでも同様に動作するかは不明。
あと、大抵の場合にはCDドライブついてるのでそちらを利用するととても便利。
また、外付けCDドライブでもインストール可能みたいなので持っているならそちらを利用。
この記事は
「CDドライブの付いていないPCに外付けCDドライブを購入することなくUbuntuをインストールする」
ためのものです。
また、作業をUbuntuで行なっているのでMacに無いコマンドがあるかも…。
本題。
簡単な流れは、
1.Macでのセットアップ
2.USBインストールメディアの作成
3.インストール
となってます。
詳しくは以下。
1.Macを起動し、rEFItをインストール
rEFItをインストールすることで、起動時にOSやUSBメモリを選択することが可能になります。
インストールはこのあたり(http://refit.sourceforge.net/)から出来ます。
2.パーティションの分割
Macの上部のメニューから移動→ユーティリティ→HDD(SSD)のパーティションを選択。
Mac側を適当に減らして空き領域を作る。
この際、「Mac,空き領域,空き領域(4GB)」のように、4GB程度(実際にはメモリの2倍だっけ)のスワップ領域を作成することが推奨されてますが、なくても問題なく動くという話もあります。
3.Ubuntuインストールメディアの作成
まず、公式(http://www.ubuntu.com/download/desktop)からUbuntuのisoイメージをダウンロード。64bit対応してるのかよく知らないけど32bit。
ダウンロード先はデスクトップにしておくとわかりやすいかな。
端末を開いて、
cd Desktop
など。カレントディレクトリをダウンロードしたisoイメージのあるディレクトリに移動すればOK。このディレクトリで、
hdiutil convert -format UDRW -o FILENAME.dwg FILENAME.iso
とする。
FILENAMEはisoイメージの名前。
これでisoイメージを変換する。
ここでUSBメモリを差し込む。端末から、
diskutil list
でUSBメモリのデバイス名を確認。今回は(/dev/disk1)だった。
確認できたらアンマウント。端末から
diskutil unmountdisk /dev/disk1
とするとアンマウントできる。手順2で使ったディスクユーティリティからUSBメモリのパーティションを変更。
USBメモリをフォーマットする。(FAT32で)
さっきと同様にアンマウント(されてるかも)
次のコマンドを実行。
dd if=filename.dmg of=/dev/rdisk1 bs=1m
これでUSBに書きこんでます。確認したデバイスの頭にrが付いていることに注意。
(/dev/disk1→/dev/rdisk1)
書きこみ完了まで十数分かかります。
/dev/disk1に書きこむと気が遠くなるほど長いので注意。
書き込みが終わったらUSBメモリの取り出し。
diskutil eject /dev/disk1
4.Ubuntuのインストール
作成したUSBインストールメディアを挿したまま、コンピュータを再起動。
するとrEFItにより選択画面が出てくるのでUSBメモリ(Ubuntu)を選択。
画面の流れに沿ってキーバインドなどの設定を行う。
Ubuntuのインストール先をパーティション分けした空き領域に入れる。
マウントポイントは「/」です。
同様に4GBの空き領域にはswapを設定。
両方ともフォーマットはext4でよいです。
ブートローダのインストール先を/dev/sdaに設定。
インストールの実行。
以上です。
記憶で書いてるのでなかなか間違いも多いかも。
2012年7月29日日曜日
MacbookAir2012にUbuntu
時間無いので適宜更新予定。
問題点
1.USBメモリからUbuntuのインストールの方法がわからない。
2.ファンクションキーの挙動が特殊(fnキーを押しながらだとファンクションとして動く)
3.やたらめったら落ちる。
4.発熱がすごい。
この内、3と4は熱暴走の関係で落ちていたっぽいです。
また、Ubuntu導入直後から全くファンが回転していなかったものと思われます。
1.USBからのUbuntuのインストールについて
時間があれば更新予定
2.fnキー単押しでファンクションとして動作させる
/etc/rc.local を以下のように編集。
exit 0 の前に
を追加。再起同時にたまに元の挙動になるけどご愛嬌。
2.3.発熱して落ちる
やたらと落ちるので調べてみるとchromeと相性悪いとか色々出てきた。
でもfirefoxにしても落ちる。
どうやら高負荷の時に落ちてるっぽい。
ファンが回ってないから熱で多分落ちてる。
まず、温度表示用のソフト入れる。
センサ認識。
とりあえずenter連打で、最後の質問だけyを入力。
実行。
sensors
ファンの回転数とか出てこればいいんだけど、どうやらMBA2012ではそのまま出ないみたい。
applesmc-dkmsをインストール。
/etc/modulesに追記
sudo vi /etc/modulesとかで、最後の行に
coretempとかあるので
いるかいらないかわからないけどmacfanctldをインストール。
適当に再起動。
これでファンが回ってるはず。
回転数はCPU温度によって可変のはずだけど最低2000rev/minなので、
動かなかった時のことを考えて/etc/macfanctl.confを改変。
fan_minを3000にしておいた。
これで多少安心。
以上。
USBからのインストールは今度かなー
----追記----
インストール編はこちら
http://hamachan-pon.blogspot.jp/2012/08/usbmacbookair2012ubuntu.html
問題点
1.USBメモリからUbuntuのインストールの方法がわからない。
2.ファンクションキーの挙動が特殊(fnキーを押しながらだとファンクションとして動く)
3.やたらめったら落ちる。
4.発熱がすごい。
この内、3と4は熱暴走の関係で落ちていたっぽいです。
また、Ubuntu導入直後から全くファンが回転していなかったものと思われます。
1.USBからのUbuntuのインストールについて
時間があれば更新予定
2.fnキー単押しでファンクションとして動作させる
/etc/rc.local を以下のように編集。
exit 0 の前に
echo 2 > /sys/module/hid_apple/parameters/fnmode
を追加。再起同時にたまに元の挙動になるけどご愛嬌。
2.3.発熱して落ちる
やたらと落ちるので調べてみるとchromeと相性悪いとか色々出てきた。
でもfirefoxにしても落ちる。
どうやら高負荷の時に落ちてるっぽい。
ファンが回ってないから熱で多分落ちてる。
まず、温度表示用のソフト入れる。
sudo apt-get install lm-sensors
センサ認識。
sudo sensors-detect
とりあえずenter連打で、最後の質問だけyを入力。
Do you want to add these lines automatically to /etc/modules? (yes/NO)
y
y
実行。
sensors
ファンの回転数とか出てこればいいんだけど、どうやらMBA2012ではそのまま出ないみたい。
applesmc-dkmsをインストール。
sudo apt-get install applesmc-dkms
/etc/modulesに追記
sudo vi /etc/modulesとかで、最後の行に
coretempとかあるので
coretemp
applesmc
hid_apple
みたいな感じに追記。applesmc
hid_apple
いるかいらないかわからないけどmacfanctldをインストール。
sudo apt-get install macfanctld
適当に再起動。
これでファンが回ってるはず。
回転数はCPU温度によって可変のはずだけど最低2000rev/minなので、
動かなかった時のことを考えて/etc/macfanctl.confを改変。
sudo vi /etc/macfanctl.conf
fan_minを3000にしておいた。
これで多少安心。
以上。
USBからのインストールは今度かなー
----追記----
インストール編はこちら
http://hamachan-pon.blogspot.jp/2012/08/usbmacbookair2012ubuntu.html
2012年6月20日水曜日
よく使うLaTeX文法
文章編
1.TITLEという表題をナンバリングなしでつける。
\part*{TITLE}

2.セクションをSECTIONという名前で付ける。レベル1
\section{SECTION}
3.サブセクションをSUBSECTIONという名前で付ける。レベル2
\subsection{SUBSECTION}
4.サブサブセクションをSUBSUBSECTIONという名前で付ける。レベル3
\subsubsection{SUBSUBSECTION}

2012年6月19日火曜日
UbuntuでLaTeX
台風4号で休講になって時間ができたので備忘録。
UbuntuによるLaTeXのコンパイル法。
やっぱり新しいプログラムとか書くときに一番面倒なのが開発環境の構築なので、
できるだけシンプルに、統合環境とか使わない方向で書いてみる。
インストールの概念がないのでそこで躓かない様になってる気がする。
1.まず、Ubuntuをインストール。これに関しては割愛。
2.端末を開き、以下を実行。エンターキーのあとにパスワード入力。
(入力しても何も変わらないけどEnter押すと入力したことになってる)
3.実行出来れば、同様に以下を実行。
4.同様に。
5.同様に。これでインストール終わり。
6.テキストエディタで以下をコピーしてMakefileという名前で保存。
(行はじめの字下げはスペースではなく必ずTABキーで)
長いので続き。
やっぱり新しいプログラムとか書くときに一番面倒なのが開発環境の構築なので、
できるだけシンプルに、統合環境とか使わない方向で書いてみる。
インストールの概念がないのでそこで躓かない様になってる気がする。
1.まず、Ubuntuをインストール。これに関しては割愛。
2.端末を開き、以下を実行。エンターキーのあとにパスワード入力。
(入力しても何も変わらないけどEnter押すと入力したことになってる)
sudo apt-get install make
3.実行出来れば、同様に以下を実行。
sudo apt-get install ptex-base
4.同様に。
sudo apt-get install nkf
5.同様に。これでインストール終わり。
sudo apt-get install texlive-base
6.テキストエディタで以下をコピーしてMakefileという名前で保存。
(行はじめの字下げはスペースではなく必ずTABキーで)
.SUFFIXES : .tex .dvi .pdf .ltx
PROG = Title
OBJS = Part1
CC = platex
NKF = nkf
NKFOPS = -d -e
DVIP = dvipdfmx
$(PROG).pdf : $(PROG).dvi
$(DVIP) $< #字下げ
$(PROG).dvi : $(PROG).tex
$(CC) $< #字下げ
$(PROG).tex : $(OBJS:=.tex)
.ltx.tex :
$(NKF) $(NKFOPS) $< > $@ #字下げ
clean :
$(RM) *.tex *.aux *.dvi *.log #字下げ
all :
make -B && make -B && make clean #字下げ
PROG = Title
OBJS = Part1
CC = platex
NKF = nkf
NKFOPS = -d -e
DVIP = dvipdfmx
$(PROG).pdf : $(PROG).dvi
$(DVIP) $< #字下げ
$(PROG).dvi : $(PROG).tex
$(CC) $< #字下げ
$(PROG).tex : $(OBJS:=.tex)
.ltx.tex :
$(NKF) $(NKFOPS) $< > $@ #字下げ
clean :
$(RM) *.tex *.aux *.dvi *.log #字下げ
all :
make -B && make -B && make clean #字下げ
長いので続き。
2012年3月23日金曜日
Euler法による一階常微分方程式の解法(CR回路を例に)
少し前の予告通りEuler法による微分方程式の求解を。
まず、微分方程式というのは方程式内に微分の形を含むもので、
例えば速度のみが与えられる場合にも微分方程式となると思います。
(勝手な定義してます。ごめんなさい。)
この場合、
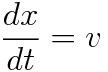
であり、両辺を積分することで
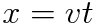
が得られます。
これが一般的な不定積分ですけど、数値解析の場合にはdxとdtを
「無限に小さな刻み幅」から少しゆるめて、
「有限の小さな値」として取り扱います。
有限になるということは普通の値と同様に扱うことができるようになります。
よって上の式を
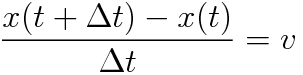
とできます。そしてこれは
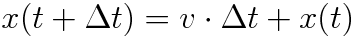
と変形できます。
ここでvは定数、Δtは任意の刻み幅なので微小時間Δtにおける変位、
x(t+Δt)-x(t)が求められます。x(t)は現在の位置です。
最後の式は微小時間が経過したあとの位置です。
一瞬前の場所x(t)に微小時間と速度を掛けたものを足した値が新しい位置となっています。
これを基本にして次の二階微分方程式を解きます。
画像多めにつき続きからどうぞ。
まず、微分方程式というのは方程式内に微分の形を含むもので、
例えば速度のみが与えられる場合にも微分方程式となると思います。
(勝手な定義してます。ごめんなさい。)
この場合、
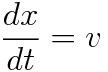
であり、両辺を積分することで
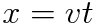
が得られます。
これが一般的な不定積分ですけど、数値解析の場合にはdxとdtを
「無限に小さな刻み幅」から少しゆるめて、
「有限の小さな値」として取り扱います。
有限になるということは普通の値と同様に扱うことができるようになります。
よって上の式を
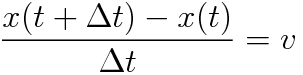
とできます。そしてこれは
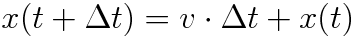
と変形できます。
ここでvは定数、Δtは任意の刻み幅なので微小時間Δtにおける変位、
x(t+Δt)-x(t)が求められます。x(t)は現在の位置です。
最後の式は微小時間が経過したあとの位置です。
一瞬前の場所x(t)に微小時間と速度を掛けたものを足した値が新しい位置となっています。
これを基本にして次の二階微分方程式を解きます。
画像多めにつき続きからどうぞ。
2012年2月23日木曜日
Newton-Roaphson法による方程式の求解
関数のグラフ化により数値解の個数とおおよその解が判別出来たところで、
その解を求めていく作業に入ります。
全部書くのは大変なのでwikipediaさんのお力を借ります。
http://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95
ニュートン法はwikipediaにもあるように、 まず、任意のx座標(wikiではxn)を決めて、
そこのy値での接線を引きます。

接線を引くと接線の傾きが0でなければ、x軸のどこかと交差します。(wikiではxn+1の点)
そのxn+1の点を再びxnとして用い、そこのy値の接線を引きます。
そしてまた接線との交点をxn+1とします。 これの繰り返しで方程式の近似解が得られます。
x軸と接線との角をθとすると、tanθは

ここで右の二式で求まっていないものはxn+1だけなのでそれを変形すると、

となるので現在分かっているxn,f(xn),f'(xn)から未知の点xn+1を求められます。
これを繰り返すと設定した点xnから大体一番近い解に収束していきます。
Newton-Roaphson法を使うにあたって必要なこと。
使用時はValue of X にそこそこ解に近い適当な値(xn)を入れてください。
forの中で10回ループしてますけど、大体そのくらいで収束します。
二つ以上の解の場合、たとえば上の図だと初期値が3以下であれば解は1くらいの値に、
3以上であれば5くらいの値に収束します。
3の場合はエラーだと思います。(接線の傾きが0のためx軸と交わらない)
以下リスト。
その解を求めていく作業に入ります。
全部書くのは大変なのでwikipediaさんのお力を借ります。
http://ja.wikipedia.org/wiki/%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95
ニュートン法はwikipediaにもあるように、 まず、任意のx座標(wikiではxn)を決めて、
そこのy値での接線を引きます。

接線を引くと接線の傾きが0でなければ、x軸のどこかと交差します。(wikiではxn+1の点)
そのxn+1の点を再びxnとして用い、そこのy値の接線を引きます。
そしてまた接線との交点をxn+1とします。 これの繰り返しで方程式の近似解が得られます。
x軸と接線との角をθとすると、tanθは

ここで右の二式で求まっていないものはxn+1だけなのでそれを変形すると、

となるので現在分かっているxn,f(xn),f'(xn)から未知の点xn+1を求められます。
これを繰り返すと設定した点xnから大体一番近い解に収束していきます。
Newton-Roaphson法を使うにあたって必要なこと。
1.方程式が判っている。(関数のグラフ化では0.5X^3 + 0.75X^2 - 2X - 2)
2.解の個数が判っている。(同じく3個)
3.接線の方程式(方程式の一階微分)が判っている。(同じく1.5X^2 + 1.5X - 2)
4.解の大体の値が判っている。
こんな感じです。2.解の個数が判っている。(同じく3個)
3.接線の方程式(方程式の一階微分)が判っている。(同じく1.5X^2 + 1.5X - 2)
4.解の大体の値が判っている。
使用時はValue of X にそこそこ解に近い適当な値(xn)を入れてください。
forの中で10回ループしてますけど、大体そのくらいで収束します。
二つ以上の解の場合、たとえば上の図だと初期値が3以下であれば解は1くらいの値に、
3以上であれば5くらいの値に収束します。
3の場合はエラーだと思います。(接線の傾きが0のためx軸と交わらない)
以下リスト。
2012年1月31日火曜日
Contents
label:電子工作
トランジスタ2石アンプ
http://hamachan-pon.blogspot.com/2011/04/blog-post.html
LT Spiceの導入
http://hamachan-pon.blogspot.com/2011/04/ltspice.html
LEDバーサライタの製作(上から順に古い)
http://hamachan-pon.blogspot.com/2011/01/led.html
http://hamachan-pon.blogspot.com/2011/03/led_23.html
http://hamachan-pon.blogspot.com/2011/04/ledmarkii.html
http://hamachan-pon.blogspot.com/2011/04/ledmarkii_05.html
DCモータのPWM制御
http://hamachan-pon.blogspot.jp/2012/08/dcpwm.html
UbuntuでのAVR開発
http://hamachan-pon.blogspot.jp/2012/11/ubuntuavr.html
STM32F4 DISCOVERYことはじめ
http://hamachan-pon.blogspot.jp/2015/09/stm32f4-discovery.html
label:ControlSystem
モータのPID制御1(サーボ制御の基礎,P制御)
http://hamachan-pon.blogspot.jp/2013/12/pid1p.html
モータのPID制御2(偏差無し制御,I制御)
http://hamachan-pon.blogspot.jp/2015/04/pid1i.html
STM32F4 DISCOVERYでのPID制御
http://hamachan-pon.blogspot.jp/2015/09/stm32f4-discoverypid.html
倒立振子シミュレーション(MATLAB/Simulink)
http://hamachan-pon.blogspot.jp/2016/01/matlabsimulink.html
多入力多出力系とは
http://hamachan-pon.blogspot.jp/2016/05/blog-post.html
シンプルな外乱オブザーバ
https://hamachan-pon.blogspot.jp/2016/10/blog-post.html
4ストロークエンジンの物理モデル
https://hamachan-pon.blogspot.jp/2017/04/4.html
カルマンフィルタの基礎式を代数とベイズ定理から見る
https://hamachan-pon.blogspot.jp/2017/04/blog-post.html
label:課題
積分の近似式(台形公式/シンプソン公式)
http://hamachan-pon.blogspot.com/2011/05/blog-post.html
ガウスの消去法(上から古い)
http://hamachan-pon.blogspot.com/2011/06/1.html
http://hamachan-pon.blogspot.com/2011/06/2.html
http://hamachan-pon.blogspot.com/2011/06/3.html
lagrange補間
http://hamachan-pon.blogspot.jp/2012/11/lagrange.html
label:Programming
C言語によるWindows用(Win32)オセロ
http://hamachan-pon.blogspot.com/2011/06/windows.html
X-Windowによる数学関数のグラフ表示
http://hamachan-on.blogspot.com/2012/01/blog-post_17.html
Newton-Roaphson法による方程式の求解
http://hamachan-pon.blogspot.com/2012/02/newton-roaphson.html
Euler法による一階常微分方程式の解法(CR回路を例に)
http://hamachan-pon.blogspot.jp/2012/03/eulercr.html
C言語でニューラルネット(関数近似)
http://hamachan-pon.blogspot.jp/2015/08/c.html
C言語でニューラルネット(2次元平面での分離)
http://hamachan-pon.blogspot.jp/2015/08/c2.html
パーティクルフィルタによるグリッドマップマッチング
http://hamachan-pon.blogspot.jp/2016/06/blog-post.html
ニューラルネットで雑な手書き文字認識
https://hamachan-pon.blogspot.jp/2016/08/blog-post.html
label:LaTeX
UbuntuでLaTeX
http://hamachan-pon.blogspot.jp/2012/06/ubuntulatex.html
よく使うLaTeX文法
http://hamachan-pon.blogspot.jp/2012/06/latex.html
label:other
MacbookAir2012にUbuntu
http://hamachan-pon.blogspot.jp/2012/07/macbookair2012ubuntu.html
http://hamachan-pon.blogspot.jp/2012/08/usbmacbookair2012ubuntu.html
2012年1月17日火曜日
数学関数のグラフ表示
今回は数学関数をX-WindowSystemでグラフ化する方法を載せたいと思います。
グラフ化することによって視覚的にわかり易くなり、実数解が存在するか程度ならすぐに分かります。
ではひとまず定義。
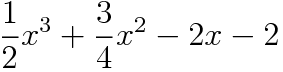
これが表示用の関数です。
ウィンドウの大きさは480*480で、うち上下左右40pxは空白部とします。
また、数値解析における分割数は100分割で、400px内を100分割して直線で結ぶ感じです。
つまり4pxは直線だけど大きい目で見たら曲線に見えるよね、って感じかな。
線を引くためには始点と終点が必要になりますが、終点は現在の計算点、始点は前回の計算点とします。
0→1、1→2、2→3点という風になります。
以下プログラムリスト。
Linuxの人はindentコマンドで整形するなりなんなりしてくだされ。
ちなみにindentコマンドは
sudo apt-get install indent
より
indent FILENAME -OPTION
で使えます。
OPTIONは-krをつかうと幸せ。
こんな感じになります。
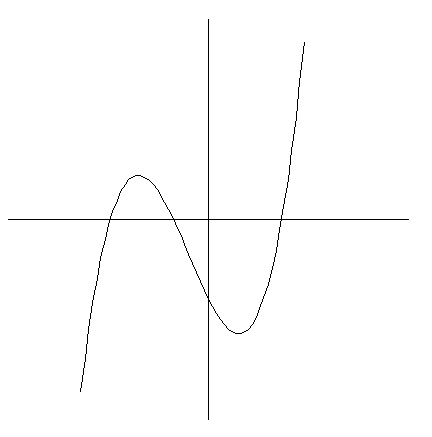
以下リスト。
グラフ化することによって視覚的にわかり易くなり、実数解が存在するか程度ならすぐに分かります。
ではひとまず定義。
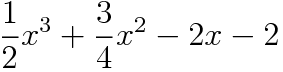
これが表示用の関数です。
ウィンドウの大きさは480*480で、うち上下左右40pxは空白部とします。
また、数値解析における分割数は100分割で、400px内を100分割して直線で結ぶ感じです。
つまり4pxは直線だけど大きい目で見たら曲線に見えるよね、って感じかな。
線を引くためには始点と終点が必要になりますが、終点は現在の計算点、始点は前回の計算点とします。
0→1、1→2、2→3点という風になります。
以下プログラムリスト。
Linuxの人はindentコマンドで整形するなりなんなりしてくだされ。
ちなみにindentコマンドは
sudo apt-get install indent
より
indent FILENAME -OPTION
で使えます。
OPTIONは-krをつかうと幸せ。
こんな感じになります。

以下リスト。
睦月
新年明けましてもう17日となりましたが、あけましておめでとうございます。
どうにか生きながらえております。
先日、成人式がありました。僕の誕生日は今月20日なので成人してるわけでは無いのですが。
中学校時代の同級生と久々に会いましたが、案外わかるもんなんですね。
望んだ理系が多くてなんか嬉しかった感じです。N氏やT氏やR氏など。
一緒に何か作れたら良いなと思ってます。
なかまになりたそうにそちらを見ます。
半期に渡る「週1でA4を10数枚」のレポートを出される授業がなんとか終わったので久しぶりの更新に至った次第です。
ちなみにこれを書いている最中にIbus標準の変換機能が悪すぎて泣いたのでmozc入れました(笑)。
sudo apt-get install ibus-mozc
で一発です。
Ibusの設定でインプットメソッドの選択→mozc→追加で使用可能です。上に持って行ってください。
少し打っただけでもすごい優秀で涙が出てきます。
閑話休題。
先程のN氏、T氏、R氏は情報理工の専門なのでちょっと(というかかなり)知識が及ばないと感じたため、逃げて専門の理工を伸ばす方向に決めたいと思います。
そこで次回からの更新予定。(すべて物理系のシミュレーションです。ちなみに開発環境はUbuntuLinux。X-WindowSystemとC言語中心です。)
1.数学関数のグラフ表示
2.Newton-Roaphson法により方程式の数値解を求める。
3.Euler法による一階常微分方程式の解法とそのグラフ化。(CR回路を例に)
4.Euler法による二階常微分方程式の解法とそのグラフ化。(ばね・ダンパ系を例に)
5.ばねによる二階常微分方程式のリアルタイムシミュレーション。
6.振り子によるに会場微分方程式のリアルタイムシミュレーション。
//7.落下、衝突のリアルタイムシミュレーション。
//8.衛生軌道のリアルタイムシミュレーション。
を考えています。
1~6は龍大理工機械の授業である通称KOJと同じモノなので載せていいか微妙なところです(笑)。まるまるコピーではないにしろCopyRightとかないのかな。
7,8はオリジナルであり作成中なので若干更新が滞る可能性があります。
また、授業ではリアルタイムシミュレーションにおいてEuler法を用いましたが、誤差が大きいため値が発散していきます。そのため同時にRunge-Kutta法でも数値計算を行う予定です。
誤差が大きいと時間が経つにつれて振り子が運動量保存則を無視して一回転したり、床でのバウンドがどんどん高くなっていったりします(笑)。
こんな感じで新年の挨拶は終わらせていただきます。
ではまた。
どうにか生きながらえております。
先日、成人式がありました。僕の誕生日は今月20日なので成人してるわけでは無いのですが。
中学校時代の同級生と久々に会いましたが、案外わかるもんなんですね。
望んだ理系が多くてなんか嬉しかった感じです。N氏やT氏やR氏など。
一緒に何か作れたら良いなと思ってます。
なかまになりたそうにそちらを見ます。
半期に渡る「週1でA4を10数枚」のレポートを出される授業がなんとか終わったので久しぶりの更新に至った次第です。
ちなみにこれを書いている最中にIbus標準の変換機能が悪すぎて泣いたのでmozc入れました(笑)。
sudo apt-get install ibus-mozc
で一発です。
Ibusの設定でインプットメソッドの選択→mozc→追加で使用可能です。上に持って行ってください。
少し打っただけでもすごい優秀で涙が出てきます。
閑話休題。
先程のN氏、T氏、R氏は情報理工の専門なのでちょっと(というかかなり)知識が及ばないと感じたため、逃げて専門の理工を伸ばす方向に決めたいと思います。
そこで次回からの更新予定。(すべて物理系のシミュレーションです。ちなみに開発環境はUbuntuLinux。X-WindowSystemとC言語中心です。)
1.数学関数のグラフ表示
2.Newton-Roaphson法により方程式の数値解を求める。
3.Euler法による一階常微分方程式の解法とそのグラフ化。(CR回路を例に)
4.Euler法による二階常微分方程式の解法とそのグラフ化。(ばね・ダンパ系を例に)
5.ばねによる二階常微分方程式のリアルタイムシミュレーション。
6.振り子によるに会場微分方程式のリアルタイムシミュレーション。
//7.落下、衝突のリアルタイムシミュレーション。
//8.衛生軌道のリアルタイムシミュレーション。
を考えています。
1~6は龍大理工機械の授業である通称KOJと同じモノなので載せていいか微妙なところです(笑)。まるまるコピーではないにしろCopyRightとかないのかな。
7,8はオリジナルであり作成中なので若干更新が滞る可能性があります。
また、授業ではリアルタイムシミュレーションにおいてEuler法を用いましたが、誤差が大きいため値が発散していきます。そのため同時にRunge-Kutta法でも数値計算を行う予定です。
誤差が大きいと時間が経つにつれて振り子が運動量保存則を無視して一回転したり、床でのバウンドがどんどん高くなっていったりします(笑)。
こんな感じで新年の挨拶は終わらせていただきます。
ではまた。