課題・ガウスの消去法1（前進消去法）

ガウスの消去法2
ガウスの消去法3

前回から授業が1回空いて、今回はガウスの消去法です。
2つ前はシンプソン公式による近似で、1つ前は改良オイラー法による常微分方程式でした。
ガウスの消去法は前進消去とか後退代入とかのやつです。
今回は前進消去だけを扱って、後退代入は次の記事になるとおもいます。

今回はこの式を題材に使います。

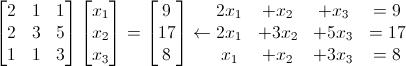
まあ簡単な連立一次方程式なんですけど、項の数が多くなってくると手計算は大変ですよね、
ということでプログラム化です。

行列についてはあまり言及しません。
学校で行くと去年の前期のことなんで忘れてるってのもありますけど＾＾；
計算自体は線形代数です。

行列式の計算は

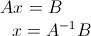
となることを利用しています。

まずは1行目を左端の2で割って、

とします。（左端を1にしたい）

次にその1行目に、「1行目の左の数が2行目の左の数になるように」定数nをかけます。
そして2行目から、n倍した1行目を引きます。するとこのように、

2行目の左端が0になりました。
（同じように3行目も1行目をn倍して引いてます。）


1行目の左端が1に、それ以外の左端が0になったので、
次は2行目2列が1になるように同じように定数（この場合では2）で割ります。



そしてその2行目を使って3行目の真ん中を0にします。（1/2をかけている）


再び、3行目の右が1になるように定数で割ります。



ここまでが前進消去です。左下に0が三角形に並んでいます。

今回はこの「前進消去」をプログラム化していきます。



これまでの流れとしては、行列をi行j列とすると、

1. 1行目の1列が1になるように1行目を割る。
   （1行目1列で1行目を割る）
2. 2行目の1列が0になるように1行目を定数倍して2行目から引く。
   （2行目マイナス、2行目1列かける1行目）
3. 3行目1列が0になるように、1行目を定数倍して3行目から引く。
   （3行目マイナス、3行目1列かける1行目）
4. 2行目2列が1になるように2行目を割る。
   （2行目2列で2行目を割る）
5. 3行目2列が0になるように、2行目を定数倍して3行目から引く。
   （3行目マイナス、3行目2列かける2行目）
6. 3行目3列が1になるように3行目を割る。

という感じです。


1~3をプログラム化すると、

int i,j,k;
double a_matrix[3][3]={{2,1,1},{2,3,5},{1,1,3}};
double b_matrix[3]={9,17,8};

/*1*/
a_matrix[0][0] = a_matrix[0][0] / a_matrix[0][0];//ここでa_matrix[0][0]が変わる
a_matrix[0][1] = a_matrix[0][1] / a_matrix[0][0];
a_matrix[0][2] = a_matrix[0][2] / a_matrix[0][0];
b_matrix[0] = b_matrix[0] /a_matrix[0][0];

/*2*/
a_matrix[1][0] = a_matrix[1][0] - a_matrix[0][0] * a_matrix[1][0];//ここでa_matrix[1][0]が変わる
a_matrix[1][1] = a_matrix[1][1] - a_matrix[0][1] * a_matrix[1][0];
a_matrix[1][2] = a_matrix[1][2] - a_matrix[0][2] * a_matrix[1][0];
b_matrix[1] = b_matrix[1] - b_matrix[0] * a_matrix[1][0];

/*3*/
a_matrix[2][0] = a_matrix[2][0] - a_matrix[0][0] * a_matrix[2][0];//ここでa_matrix[1][0]が変わる
a_matrix[2][1] = a_matrix[2][1] - a_matrix[0][1] * a_matrix[2][0];
a_matrix[2][2] = a_matrix[2][2] - a_matrix[0][2] * a_matrix[2][0];
b_matrix[2] = b_matrix[2] - b_matrix[0] * a_matrix[2][0];

と書きたいところですけど、コメントのようにその時点で使いたい数字が変更されてしまうので、
違う数値に格納しておきます。これをbufとでも付けておきます。
修正して4~6も入れたのが以下です。

修正後

int i,j,k;
double a_matrix[3][3]={{2,1,1},{2,3,5},{1,1,3}};
double b_matrix[3]={9,17,8};
double buf;

/*1*/
buf = a_matrix[0][0];
a_matrix[0][0] = a_matrix[0][0] / buf;
a_matrix[0][1] = a_matrix[0][1] / buf;
a_matrix[0][2] = a_matrix[0][2] / buf;
b_matrix[0] = b_matrix[0] /buf;

/*2*/
buf = a_matrix[1][0];
a_matrix[1][0] = a_matrix[1][0] - a_matrix[0][0] * buf;
a_matrix[1][1] = a_matrix[1][1] - a_matrix[0][1] * buf;
a_matrix[1][2] = a_matrix[1][2] - a_matrix[0][2] * buf;
b_matrix[1] = b_matrix[1] - b_matrix[0] * buf;

/*3*/
buf = a_matrix[2][0];
a_matrix[2][0] = a_matrix[2][0] - a_matrix[0][0] * buf;
a_matrix[2][1] = a_matrix[2][1] - a_matrix[0][1] * buf;
a_matrix[2][2] = a_matrix[2][2] - a_matrix[0][2] * buf;
b_matrix[2] = b_matrix[2] - b_matrix[0] * buf;

/*4*/
buf = a_matrix[1][1];
a_matrix[1][0] = a_matrix[1][0] / buf;
a_matrix[1][1] = a_matrix[1][1] / buf;
a_matrix[1][2] = a_matrix[1][2] / buf;
b_matrix[1] = b_matrix[1] /buf;

/*5*/
buf = a_matrix[2][1];
a_matrix[2][0] = a_matrix[2][0] - a_matrix[1][0] * buf;
a_matrix[2][1] = a_matrix[1][1] - a_matrix[1][1] * buf;
a_matrix[2][2] = a_matrix[1][2] - a_matrix[1][2] * buf;
b_matrix[2] = b_matrix[2] - b_matrix[1] * buf;

/*6*/
buf = a_matrix[2][2];
a_matrix[2][0] = a_matrix[2][0] / buf;
a_matrix[2][1] = a_matrix[2][1] / buf;
a_matrix[2][2] = a_matrix[2][2] / buf;
b_matrix[2] = b_matrix[2] /buf;

これで一応の答えは出たかなー？
まあご周知の通りこんなプログラム汎用性がないわけです。
行列増やしたらまた打ち直しとか。

そんなわけでここからループ化していきます。
実際、自分がプログラムに書くのってここからなんですけど＾＾；

まず、感じとしては、同じ一連の数字のところに同じ変数を入れます。
その前に、プログラムとして同じ処理を見極めます。

手順1と4,6はbufで割る計算、2,3,5はaにbufをかけてaから引く計算です。
なので順番は1→2,3→4→5→6とします。

手順1のbuf = a[0][0];を手順4,6と比べてみると、[0][0]と[1][1],[2][2]であることがわかります。
なので両方同じように増えるのでa[i][i]と置いてみます。
ループとして書くと、

for(i = 0;i < 3;i++){
/*処理*/
}

そして、aをbufで割る計算のところは、aの左側がiと同じ、右側は0~2と増えていきます。
右側をjと置きます。右側をjと置くと、jは0,1,2なので

for(j = 0;j < 3;j++){
/*処理*/
}

とすればいいように思います。
以下は実行しないでください。

int i,j,k;
double a_matrix[3][3]={{2,1,1},{2,3,5},{1,1,3}};
double b_matrix[3]={9,17,8};
double buf;

/*1*/
for(i = 0;i < 3;i++){
buf = a_matrix[i][i];
for(j = 0;j < 3;j++){
a_matrix[i][j] = a_matrix[i][j] / buf;
}
b_matrix[i] = b_matrix[i] /buf;/*何度も割ってはいけないのでjの外に出す*/
}

/*2*/
buf = a_matrix[1][0];
a_matrix[1][0] = a_matrix[1][0] - a_matrix[0][0] * buf;
a_matrix[1][1] = a_matrix[1][1] - a_matrix[0][1] * buf;
a_matrix[1][2] = a_matrix[1][2] - a_matrix[0][2] * buf;
b_matrix[1] = b_matrix[1] - b_matrix[0] * buf;

/*3*/
buf = a_matrix[2][0];
a_matrix[2][0] = a_matrix[2][0] - a_matrix[0][0] * buf;
a_matrix[2][1] = a_matrix[2][1] - a_matrix[0][1] * buf;
a_matrix[2][2] = a_matrix[2][2] - a_matrix[0][2] * buf;
b_matrix[2] = b_matrix[2] - b_matrix[0] * buf;

/*5*/
buf = a_matrix[2][1];
a_matrix[2][0] = a_matrix[2][0] - a_matrix[1][0] * buf;
a_matrix[2][1] = a_matrix[1][1] - a_matrix[1][1] * buf;
a_matrix[2][2] = a_matrix[1][2] - a_matrix[1][2] * buf;
b_matrix[2] = b_matrix[2] - b_matrix[1] * buf;

次に、手順2,3,5を考えます。
2,3,5ともに1と同じくaの右は0~2です。
2,3ともに左側は1~2です。
しかし5では左側が2のみです。

この場合では手順2,3をペアに、5をひと固まりとして考えます。

手順2,3ではiの値は0で、aの左は1~2です。
手順5ではiの値は1で、aの左は2です。

こうすると、aの左はi+1から始まり、2で終われば良いように思います。
これはb_matrix[i] = b_matrix[i] /buf;の下に書かなければいけないため、
さっきのjループの外側です。なのでもう一度、変数jを利用します。

その中にまたループを作ってaの右を0~2しなくてはいけないので、
同じようにkでループを作ります。

for(j = i+1;j < 3;j++){
for(k = 0;k < 3;k++){
/*処理*/
}
}

これらすべてをプログラムとして完成させると、

#include<stdio.h>

/*prototype*/
int PRINT(double a_matrix[3][3],double b_matrix[3]);

int main(void){
int i,j,k;
double a_matrix[3][3] = {{2,1,1},{2,3,5},{1,1,3}};
double b_matrix[3] = {9,17,8};
double buf;

PRINT(a_matrix,b_matrix);

for(i = 0;i < 3;i++){
buf = a_matrix[i][i];
for(j = 0;j < 3;j++){
a_matrix[i][j] = a_matrix[i][j] / buf;
}
b_matrix[i] = b_matrix[i] / buf;

for(j = i + 1;j < 3;j++){
buf = a_matrix[j][i];
for(k = 0;k < 3;k++){
a_matrix[j][k] = a_matrix[j][k] - a_matrix[i][k] * buf;
}
b_matrix[j] = b_matrix[j] - b_matrix[i] * buf;
}
}
PRINT(a_matrix,b_matrix);
return 0;
}

int PRINT(double a_matrix[3][3],double b_matrix[3]){
int i,j;
for(i = 0;i < 3;i++){
for(j = 0;j < 3;j++){
printf("%6.4f ",a_matrix[i][j]);
}
printf("%6.4f\n",b_matrix[i]);
}
printf("\n");
return 0;
}

となります。
これで前進消去は完成です。
PRINTは行列を表示するためのサブルーチンです。

後退代入も同じような手段なのでここまで書ければ簡単だと思います。
それとループの打ち切り数3は変更がきくように変数に書き換えておくと便利かと思います。
同じく行列も50x50くらいで作っておくと、項の数が多くなっても融通がききます。

次回は後退代入とピボット（の予定）です。

おつさまですた。