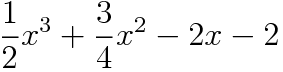label:電子工作
トランジスタ2石アンプ
http://hamachan-pon.blogspot.com/2011/04/blog-post.html
LT Spiceの導入
http://hamachan-pon.blogspot.com/2011/04/ltspice.html
LEDバーサライタの製作(上から順に古い)
http://hamachan-pon.blogspot.com/2011/01/led.html
http://hamachan-pon.blogspot.com/2011/03/led_23.html
http://hamachan-pon.blogspot.com/2011/04/ledmarkii.html
http://hamachan-pon.blogspot.com/2011/04/ledmarkii_05.html
DCモータのPWM制御
http://hamachan-pon.blogspot.jp/2012/08/dcpwm.html
UbuntuでのAVR開発
http://hamachan-pon.blogspot.jp/2012/11/ubuntuavr.html
STM32F4 DISCOVERYことはじめ
http://hamachan-pon.blogspot.jp/2015/09/stm32f4-discovery.html
label:ControlSystem
モータのPID制御1(サーボ制御の基礎,P制御)
http://hamachan-pon.blogspot.jp/2013/12/pid1p.html
モータのPID制御2(偏差無し制御,I制御)
http://hamachan-pon.blogspot.jp/2015/04/pid1i.html
STM32F4 DISCOVERYでのPID制御
http://hamachan-pon.blogspot.jp/2015/09/stm32f4-discoverypid.html
倒立振子シミュレーション(MATLAB/Simulink)
http://hamachan-pon.blogspot.jp/2016/01/matlabsimulink.html
多入力多出力系とは
http://hamachan-pon.blogspot.jp/2016/05/blog-post.html
シンプルな外乱オブザーバ
https://hamachan-pon.blogspot.jp/2016/10/blog-post.html
4ストロークエンジンの物理モデル
https://hamachan-pon.blogspot.jp/2017/04/4.html
カルマンフィルタの基礎式を代数とベイズ定理から見る
https://hamachan-pon.blogspot.jp/2017/04/blog-post.html
label:課題
積分の近似式(台形公式/シンプソン公式)
http://hamachan-pon.blogspot.com/2011/05/blog-post.html
ガウスの消去法(上から古い)
http://hamachan-pon.blogspot.com/2011/06/1.html
http://hamachan-pon.blogspot.com/2011/06/2.html
http://hamachan-pon.blogspot.com/2011/06/3.html
lagrange補間
http://hamachan-pon.blogspot.jp/2012/11/lagrange.html
label:Programming
C言語によるWindows用(Win32)オセロ
http://hamachan-pon.blogspot.com/2011/06/windows.html
X-Windowによる数学関数のグラフ表示
http://hamachan-on.blogspot.com/2012/01/blog-post_17.html
Newton-Roaphson法による方程式の求解
http://hamachan-pon.blogspot.com/2012/02/newton-roaphson.html
Euler法による一階常微分方程式の解法(CR回路を例に)
http://hamachan-pon.blogspot.jp/2012/03/eulercr.html
C言語でニューラルネット(関数近似)
http://hamachan-pon.blogspot.jp/2015/08/c.html
C言語でニューラルネット(2次元平面での分離)
http://hamachan-pon.blogspot.jp/2015/08/c2.html
パーティクルフィルタによるグリッドマップマッチング
http://hamachan-pon.blogspot.jp/2016/06/blog-post.html
ニューラルネットで雑な手書き文字認識
https://hamachan-pon.blogspot.jp/2016/08/blog-post.html
label:LaTeX
UbuntuでLaTeX
http://hamachan-pon.blogspot.jp/2012/06/ubuntulatex.html
よく使うLaTeX文法
http://hamachan-pon.blogspot.jp/2012/06/latex.html
label:other
MacbookAir2012にUbuntu
http://hamachan-pon.blogspot.jp/2012/07/macbookair2012ubuntu.html
http://hamachan-pon.blogspot.jp/2012/08/usbmacbookair2012ubuntu.html