制御系の研究ではお馴染みの倒立振子のシミュレーションをやってみます.
動画はシミュレーションの様子.
実は,ToolBoxにSimscapeというものがありまして,その中のSimMechanicsではMATLAB上で3Dソリッドモデルを作るだけで物理シミュレーションができたりします.
ただし,今回は普通のSimulinkのみで行います(笑)やっぱり解析的に色々するには,どちらにしろ運動方程式も立てないといけないので.
大体の場合において,制御をしようと思うと,運動方程式のパラメータから
制御系の設計パラメータを求める必要が出てきます.
そんな理由から,運動方程式を立てて,制御パラメータを決めていく方法で今回は制御系の設計を行います.
まずは倒立振子の運動方程式から.倒立振子にも色々ありますが,今回は車輪型についてです.
製品では,ヴィストン株式会社のbeuto balancerなどがあります.
下の図のように,車輪と振り子部分から構成されていて,下の車輪が動くことで上の本体のバランスをとって倒立させるというものです.
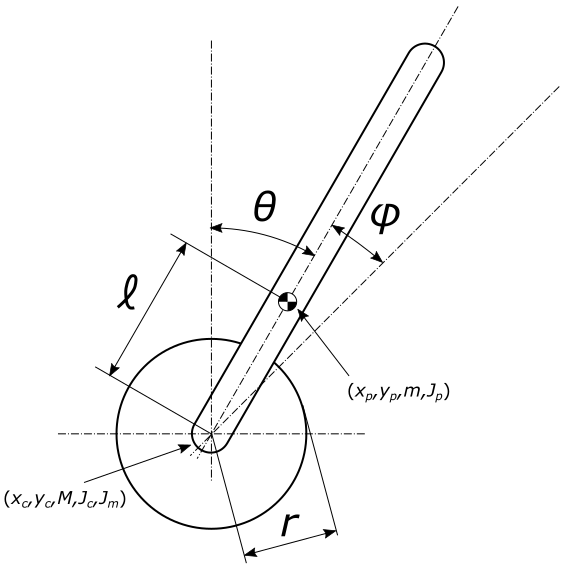
制御すべきは,本体の位置と角度で,入力は車輪にあるモータへのトルク入力となっています.
つまりは,モータのトルク入力(電流入力)を与えて,倒立振子を倒さずに好きなところに移動させるという制御です.
ここで,は本体の地面に対する角度,は初期タイヤ角度からの変位量です.
に関しては,ロボットの特性上,角度センサで地面との相対角度を取得して,ロータリーエンコーダでタイヤの回転角度を取得することが多いのでこのような設定としています.
(ロータリーエンコーダでは基本的にプログラム実行時の初期角度からの変化量しか取得できないので.)
この運動方程式の導出方法はいろいろあるかと思いますが,今回はラグランジュ法を使用していきます.
- まず,タイヤの回転軸中心に関しては次の関係が得られます.
- 次に,振子部分の重心位置について,以下の関係が得られます.
- これらの関係から,振り子部分の並進方向の運動エネルギは,
- 振り子の回転方向の運動エネルギは,
- タイヤの並進方向の運動エネルギは,
- タイヤの回転方向の運動エネルギは,
- モータ電機子の回転エネルギは以下のように求められます.
ここで,はモータの減速比です.
よって,系全体の運動エネルギ,位置エネルギ,散逸エネルギは,以下のように得られます.
ここから,ラグランジアンを求めます.(長い)
これより,ラグランジアンの変数ごとの偏微分を求めます.まずは変数について.
次に変数について.
これまでにラグランジアンの偏微分が全て求まったので,運動方程式を導出します.まず,変数についての式から,
次に,変数についての式から,
これで,車輪型倒立振子の運動方程式の導出が完了しました.このままでは使い勝手が悪いので,まずは倒立状態付近かつ,静止状態で線形化します.
ただし,はモータに流れる電流,はモータのトルク定数であり,は入力トルクを表します.
このとき,,です.
次に,状態方程式(行列形式)ベースに書き直します.
ただし,
更に変形して,
これらをまとめると,以下の状態方程式が得られます.
ただし,
[kg],[kg],
[kgm],[kgm],[kgm],
[m],[m],,,
次に,制御系の設計について.今回は単純な状態フィードバックを使用しますが,この場合,全状態変数が観測できる必要があります.
現実には,ロボット本体の角度とタイヤの角度を測定し,他の2変数は推定することが多いかと思いますが,
シミュレーションですので,ここでは全状態変数が観測可能なものとして扱います.
つまり,状態方程式のおよびの項は以下のとおりです.
状態フィードバックの係数は,最適制御で行います.
最適制御では,各状態変数と入力に対する「重み」を設定して,以下の評価関数が最小となるような状態フィードバックの係数を求めます.
状態変数に対する重みは,入力に対する重みはで表すことが多いかと思います.
今回は,例として以下のとを設定しました.
このように表記した場合,の左上からそれぞれ,,,,に対する重みとなっています.
つまり,車体の角度を素早くゼロに近づけ,安定化させることを重要視した重み,ということになります.
また,は入力に対する重みで,これを大きくすると入力をできるだけ小さく抑えたい,ということに相当します.
(このあたりの記述はあまり正確ではないかもしれません.)
MATLABを使う場合,この最小化は関数として用意されているので,次の記述だけで済みます.
gain = lqr(A, B, Q, R);ここから,状態フィードバックの係数が
gainとして得られます.gain = [-6.6700 -0.0447 -1.0000 -0.0583]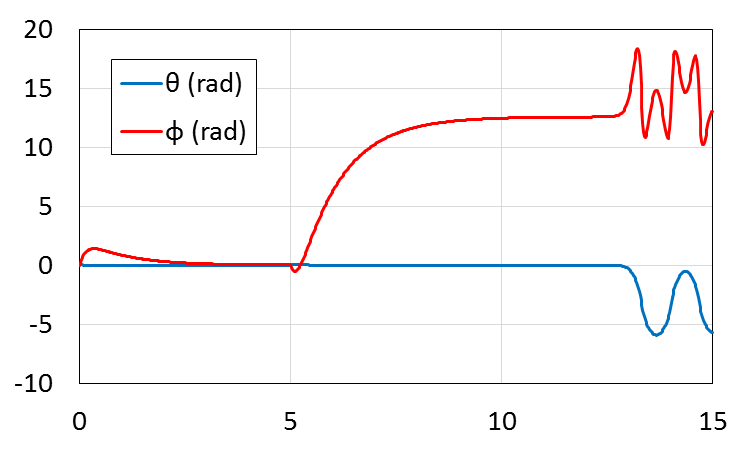
しっかりと安定化でき,目標の位置にも追従できていることがわかります.
12秒時点で入力を切っているため,そこからは転倒してしまっています.
トップの動画は,これをProcessingで可視化したものです.
倒立振子の安定化制御はわりと色んな所で見るので試しにやってみた次第です.
近いうちに実機の方にも実装できるといいなあ.
9 件のコメント:
最後のシミュレーションでは、プラントモデルは
θ≒0, θ'≒0の近似を行う前のもので計算していますか?
入力を切ったあとの挙動が、提示されているものと一致しなくて…。
よろしければどの様にモデリングしているのか教えていただければ幸いです。
匿名さん
はじめまして.Hamachiです.
仰るとおり,シミュレーションは近似前の式で実装しています.
近似後の式を利用すると発散するのでしょうか?
近似の直前に,φに関する式から~と,θに関する式から~という部分がありますが,
シミュレーションではこれを変形して使用しています.
具体的には2式を連立させて,φの2階微分と,θの2階微分について解き,以下の形式にします.
ddφ = Adφ + Bφ + Cdθ + Ddθ
ddθ = Edφ + Fφ + Gdθ + Hdθ
ddφはφの時間に関する2階微分,dφは1階微分,A~Hは定数です.
手動での導出はそれなりに大変なので,私はMaximaなどを使っています.
参考
https://hamachannel.hatenablog.com/entry/2018/01/14/120848#wxMaxima%E3%81%AB%E3%82%88%E3%82%8B%E9%81%8B%E5%8B%95%E6%96%B9%E7%A8%8B%E5%BC%8F%E5%B0%8E%E5%87%BA
2階微分の形式が得られたら,Euler法やRunge-Kutta法で離散近似すると,
非線形システムとしてのシミュレーションができるかと思います.
このときはMATLAB/Simulink標準のDormand-Princeだったように思います.
ご不明点などあればご連絡頂けると夜には落ち着いてご回答できるかと思います.
取り急ぎ,お返事まで.
Hamachiさん
ご返事ありがとうございました.
同じ結果になりました!
このページも参考ページも非常に勉強になりました.
ご対応ありがとうございました.
匿名さん
解決されたようで良かったです!
Hamachi様
はじめまして、相馬と申します。
制御工学の勉強のために倒立振子を作成しており、
本ページを参考にさせていただいてます。
そこで本記事に関し一点、質問がございます。
「7.モータ電機子の回転~」の式で初めて登場する
「i」とは、何のことを指していますでしょうか。
もし宜しければ、ご回答いただきますと幸いです。
相馬さん
はじめまして,Hamachiと申します.
あまり上等な記事ではありませんが,見ていただきありがとうございます.
見直してみたところ,たしかにiについて全く言及していませんでした.
ご不便をおかけしております.
iは,モータの減速比を表しています.
モータの軸の回転角度(速度)からタイヤの回転角度(速度)までは,モータに減速比が設定されている場合,i倍になるためです.
回転方向の完成もi倍されるため,このような項が現れています.
ついでにaについても言及していないようでしたのでここで.
回転方向の運動方程式 = au となっていることから,auはトルク(N.m)を表します.
例えばuを電流とすると,aはモータのトルク定数(逆起電力定数)を指すことになります.
分かりづらい説明で恐縮ですが,宜しくお願い致します.
Hamachi様
ご返信いただき、ありがとうございました。
iは減速比なのですね。式全体、それから単位を考えると
無次元量のようなので、納得しました。
auについても、丁度疑問に感じていたところでしたので
助かりました。ありがとうございます。
それと、恐れ入りますが、もう2点。
もし間違いでしたら申し訳ないですが、
①「ここから、ラグランジアンL=~」以下の式において、
-mgcosθとなっている個所は、正しくは-mglcosθでしょうか。
(下の方の式です)
②「これより,ラグランジアンの変数ごとの~」以下の
「次に変数θについて.」以下の
「∂L/∂θ・」の式において、(θ・→シートドットと思って下さい)
4つ目の項がml^2θ・^2sin^2θとなっていますが、正しくは
ml^2θ・sin^2θでしょうか。
(真下の時間微分している場合も同様)
以上、お手数ですが、ご確認いただけますと助かります。
(学習のため1つ1つ計算したところ、上記を発見して気になりました。
細かくて申し訳ないです。。)
相馬
相馬さん
Hamachiです.
いろいろご指摘ありがとうございます.
改めて見直すと穴だらけですね……
①,②について仰る通りです.
①については"l"は後の式で復活しているので恐らく書き忘れです.
②については ∂L/∂dθのところ(dθは時間微分)は間違っていそうです.
ラグランジアンLのところで ( l^2 * θ^2 * cosθ^2 ) + ( l^2 * θ^2 * sinθ^2 ) は簡約化されて ( l^2 * θ^2 ) になるはずなので,そもそも消えていないのが変ですね.
ただ,これを時間微分したもの(d/dt(∂L/∂θ))については合っているような気がします.
( 2 * m * l^2 * dθ^2 * sinθ * cosθ ) は正負で2つ出現し,相殺されるはずです.
実際,上記の簡約化をした後に時間微分をすると,そもそも出現しないことが確認できるかと思います.
実は当時使っていたブログの編集サイトが閉鎖してしまい,修正に時間がかかりそうなのでその点ご容赦いただけると幸いです.
一応,Maximaという数式処理ソフトで計算してみたので,よろしければ参考にご覧ください.
パスワードはHamachiです.
http://whitecats.dip.jp/up/download/1558582929/attach/1558582929.pdf
pdfの基となったMaximaのファイルもありますので,ご入用であればご連絡いただければと思います.
Hamachi様
ご返信いただき、ありがとうございました。
>ただ,これを時間微分したもの(d/dt(∂L/∂θ))については合っているような気がします.
大変失礼致しました。此方でも再計算したところ、上掲の式が正しいことを確認しました。
>実は当時使っていたブログの編集サイトが閉鎖してしまい,修正に時間がかかりそうなので
>その点ご容赦いただけると幸いです.
大丈夫です、正しい式を確認するのが目的でしたし、Hamachi様からの返信でその目的は達成
できましたので。
>一応,Maximaという数式処理ソフトで計算してみたので,よろしければ参考にご覧ください.
ありがとうございます、参考にさせていただきます。
>pdfの基となったMaximaのファイルもありますので,ご入用であればご連絡いただければと思います.
重ね重ね、ありがとうございます。必要になった場合、再度連絡させていただきます。
相馬
コメントを投稿