外乱オブザーバ(Disturbance observer; DOB)はフィードバックシステムに外乱が加わるような状況で,比較的簡単に外乱を除去し安定化できる強力なツールですが,ウェブにはあまり記述が無いようだったので書いてみました.
- 外乱オブザーバとは?
- なぜ外乱オブザーバが必要なのか
- 基本原理
- 実際の外乱オブザーバ(ノミナルモデル,ローパスフィルタ)
そもそも外乱オブザーバとは?
“外乱”でググってみると,以下のような説明が得られます.
ある通信系に、所定の信号系以外から加わり妨害となる信号。 --- 大辞林大体内容としては間違いないですが,今回扱うのは”通信系”に限らず,制御システムに対してはたらく,妨害となる信号くらいに留めておきます.
外乱オブザーバとは,このような外乱を除去するために,制御系のコントローラに組み込む補償器のひとつです.
なぜ外乱オブザーバが必要なのか
次のような1次遅れ系のフィードバックループを考えてみます.

ここで,はコントローラ,は制御対象です.また,目標値を,出力をで表します.
外乱というと,図の1, 2, 3番の箇所に加わることが想定されますが,本稿では1について記述します.
また,以下の理由で2, 3番を省いています.
2番の部分に入力される外乱は,フィードバックループを構成する主な目的のひとつのため,比較的簡単に除去(補償)できる.
3番については,システム自体は目標値通り動作している(外乱によって我々使用者が目標値どおりに動作しているか確認できないだけの状態)ため.1番は,コントローラは制御対象を最適に動作させるための操作量を正常に生成できているが,それが外乱によって変えられ制御対象に入力されてしまっている状態です.
つまり,PIDなどのコントローラを適切に設計しても,設計通りの操作量が制御対象に入力されないということです.
今回はこの外乱を除去する外乱オブザーバについて述べていきます.
ここでは,"最適な操作量"は設計時に想定している操作量を指します.
最適レギュレータなどの最適とは根本的に異なる内容ですのであしからず.基本的な原理
上述のように,外乱が1番の部分に入力される場合,ブロック図は以下のようになります.

このとき,制御対象の出力は,
このように,コントローラによって計算された最適な入力が,外乱によって変えられてしまいます.
これによって,システムが上手く制御できないということが稀にあります.
たとえば,モータを電流制御のため,モータドライバを使った場合,入力の電圧信号に対して電流にオフセットが出ることがあります.
この場合も,入力側の外乱が発生しているのと同じ意味となります.
そこで,コントローラで生成された操作量から,あらかじめ外乱を引いておけば入力側外乱の影響を除去することができます.
これを図で書くと以下のようになります.
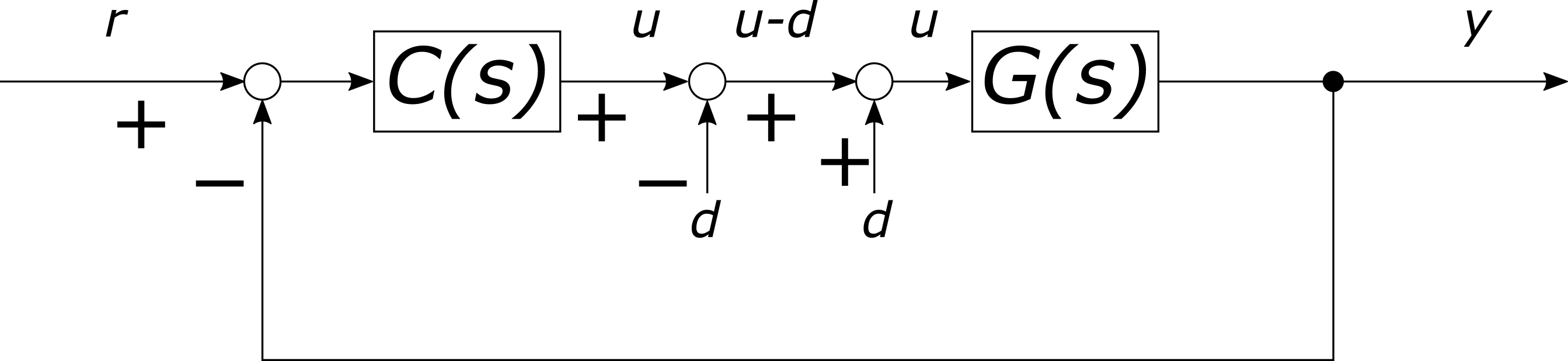
このときの出力は,
非常に当たり前の話ですが,外乱がわかっていればこれだけで外乱を除去できます.
問題は,どうやって外乱を推定するのかということです.
外乱が完全に推定できるなら,フィードバック制御なんてものは必要ないはずです.
コントローラは外乱より先にあるため,外乱がどのようなものか推定することはできませんが,出力側では,外乱の影響を受けたあとの出力となっているため,ここから推定できそうです.
上述のように,外乱の影響を受けたシステムの出力は,
ですので,制御対象の逆システムが存在すれば,両辺にこれをかけて,
となり,外乱を推定できます.ここでは推定外乱で,ハットを付けています.
これをブロック線図で次のように表せます.

コントローラによって生成された操作量は,推定外乱と外乱を受けてとなるため,
システムの出力は,
となります.ここから,推定外乱は,
ここで制御対象とその逆システムの積とすると,以下が成り立ちます.
このような原理により,外乱を推定し,除去することができます.
実際の外乱オブザーバはどうなっているのか
これまでは,制御対象の逆システムが得られるという条件で導出を行ってきました.
しかし実際には制御対象の逆の応答をするようなシステムを得ることはできません.
このため,プログラム上で制御対象の伝達関数を生成し使用します.
このような制御方式をモデル規範型制御と呼んだりもするようです.
たとえば,制御対象が1次遅れ系と近似できそうな場合には,
とでも置き,逆システムを以下のように定義します.
基本的には外乱オブザーバを使用する際にはこのように規範モデル(Nominal model)を導出し使用する流れとなります.
外乱オブザーバを使用するメリット,デメリットとしては以下のようになります.
メリット
- 除去の比較的困難な入力側の外乱を除去できる.
- 制御対象と規範モデルとのモデル化誤差も補償できる.
- 能動的に外乱を除去するため,外乱入力からの反応が速い.
デメリット
- 規範モデルを導出する必要がある.
- 実用上はローパスフィルタを併用する必要がある.
モデル化誤差については,制御対象とノミナルモデルの特性が少し違っていても安定に動作するという意味です.
それなりに1次遅れっぽい応答をするな,というような制御対象でも1次遅れで近似してパラメータを決めてやると大体の場合,上手く動作します.
また,他の外乱除去手法では過去の誤差から外挿によって外乱を除去する方法がありますが,このような手法に比べて反応が速く使い勝手がよいです.
反対に,制御対象の反応を見ながらチューニングし,ブラックボックスをそのまま制御できるPIDなどにおいては,わざわざ制御対象のモデル化をしなければならないという圧倒的なデメリットが有ります.
しかしこれについては,近年ではPIDでも制御対象をモデル化し,シミュレーションをしながらパラメータを決定する場合が多くありますし,そもそも制御に内部モデルを使用するモデル規範型の制御も増えてきています.
このような場合には,モデルをそのまま使えば良いのでほとんど面倒はないです.
最後のローパスフィルタが一番の面倒で,実用上はフィルタの設計とパラメータのチューニングが必須になってきます.外乱オブザーバを使用する上で,気をつけたいのがフィルタの設計です.
逆システムの式を見てわかるように,微分項が含まれています.
微分動作は基本的に不安定な要素のため,これを避けるためにローパスフィルタを使用します.
使いやすいところだと,Butterworthのフィルタがあります.
カットオフ周波数をとすると,フィルタの伝達関数は以下となります.
これを推定外乱にかけたものをよく見かけますが,これではやはり微分器が必要となってしまいます.
ここでは微分器を使いたくないので,ローパスフィルタを分割して以下のように配置します.

すると,出力側からの項が次のように書き換えられ,微分要素を排除することができます.
このように分母次数より分子の次数の方が小さくなったため,は安定に(というと語弊がありそうですが)動作します.
MATLAB/Simulinkでシミュレーションする際には,逆システムをそのまま伝達関数としては使えないためこのような方法を使うことになります.
実際のフィルタのカットオフ周波数についてはHzくらいに設定することが多いのではないかと.
これは実際のプロセスで検証しつつ決定します.
今回,フィルタは2次のButterworthフィルタを使っていますが,実際にはなんでも良いです.
Butterworthフィルタはリップルがないため,特定の周波数帯で共振したりということがなく使いやすいのでほとんどこれしか使ったことありません.
コントローラをPID,制御対象を1次遅れ系としたときの動作が次のようになります.
制御対象の時定数をs,DOB用フィルタのカットオフ周波数はHzに設定しています.

この図ではsに入力側外乱,sに出力側外乱を与えています.
このように外乱オブザーバをつかうことで強力に外乱を除去できることがわかるかと思います.
1 件のコメント:
分かりやすくて理解できました。ありがとうございます。
コメントを投稿