まず、微分方程式というのは方程式内に微分の形を含むもので、
例えば速度のみが与えられる場合にも微分方程式となると思います。
(勝手な定義してます。ごめんなさい。)
この場合、
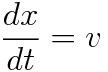
であり、両辺を積分することで
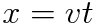
が得られます。
これが一般的な不定積分ですけど、数値解析の場合にはdxとdtを
「無限に小さな刻み幅」から少しゆるめて、
「有限の小さな値」として取り扱います。
有限になるということは普通の値と同様に扱うことができるようになります。
よって上の式を
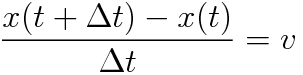
とできます。そしてこれは
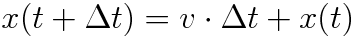
と変形できます。
ここでvは定数、Δtは任意の刻み幅なので微小時間Δtにおける変位、
x(t+Δt)-x(t)が求められます。x(t)は現在の位置です。
最後の式は微小時間が経過したあとの位置です。
一瞬前の場所x(t)に微小時間と速度を掛けたものを足した値が新しい位置となっています。
これを基本にして次の二階微分方程式を解きます。
画像多めにつき続きからどうぞ。